
Projekt jest prostym edukacyjnym eksperymentem polegającym na wyznaczeniu współczynnika tarcia za pomocą pomiaru zmieniającej się odległości zjeżdżającego klocka po równi pochyłej.
1. Płytka NodeMCU (ESP8266)
2. Czujnik HC-SR04
3. Wyświetlacz OLED I2C
4. płytka stykowa
5. 4 przewody męsko-męskie
6. 3 przewody męsko-żeńskie
7. 1 przewód żeńsko-żeński
1. Komputer PC z oprogramowaniem Thonny
2. Rampa
3. Klocek
4. Linijka, miarka lub kątomierz
Jak już zostało napisane wcześniej celem projektu jest wyznaczanie współczynnika tarcia na równi pochyłej, w tym celu wykorzystamy prosty układ złożony z płytki esp8266, dalmierza ultradźwiękowego HC-SR04 oraz wyświetlacza OLED i2c.
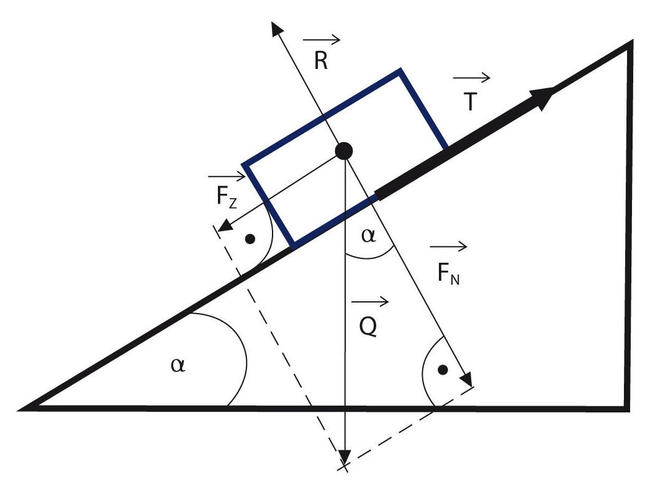
Do obliczenia ów współczynnika wykorzystamy proste zależności dla równi pochyłej
1. II zasada dynamiki Newtona
Fw = m*a z czego wynika następujące równanie:
m*a = m*g*sin(alfa) - m*g*u*cos(alfa) z tego równania dalej możemy wyznaczyć wzór na współczynnik tarcia:
u = tg(alfa) - (a/(g*cos(alfa)))
Przy założeniu, że wiemy ile wynosi przyspieszenie grawitacyjne oraz jak zbudowana jest rampa(jeśli nie wiemy z pomocą przyjdzie nam miarka lub kątomierz), pozostaje nam tylko wyznaczenie przyspieszenie zjeżdżającego klocka. Tu z pomocą przychodzi nam nasz układ który oblicza ów przyspieszenie. Program korzysta ze znanej licealnej formuły na drogę w ruchu przyspieszonym:
2. s = 0.5*a*t^2 + v0*t + s0
Przy założeniu że klocek nie ma lub ma bardzo niską prędkość początkową równanie możemy uprościć do:
s = 0.5*a*t^2 gdzie a = (2*s/t^2)
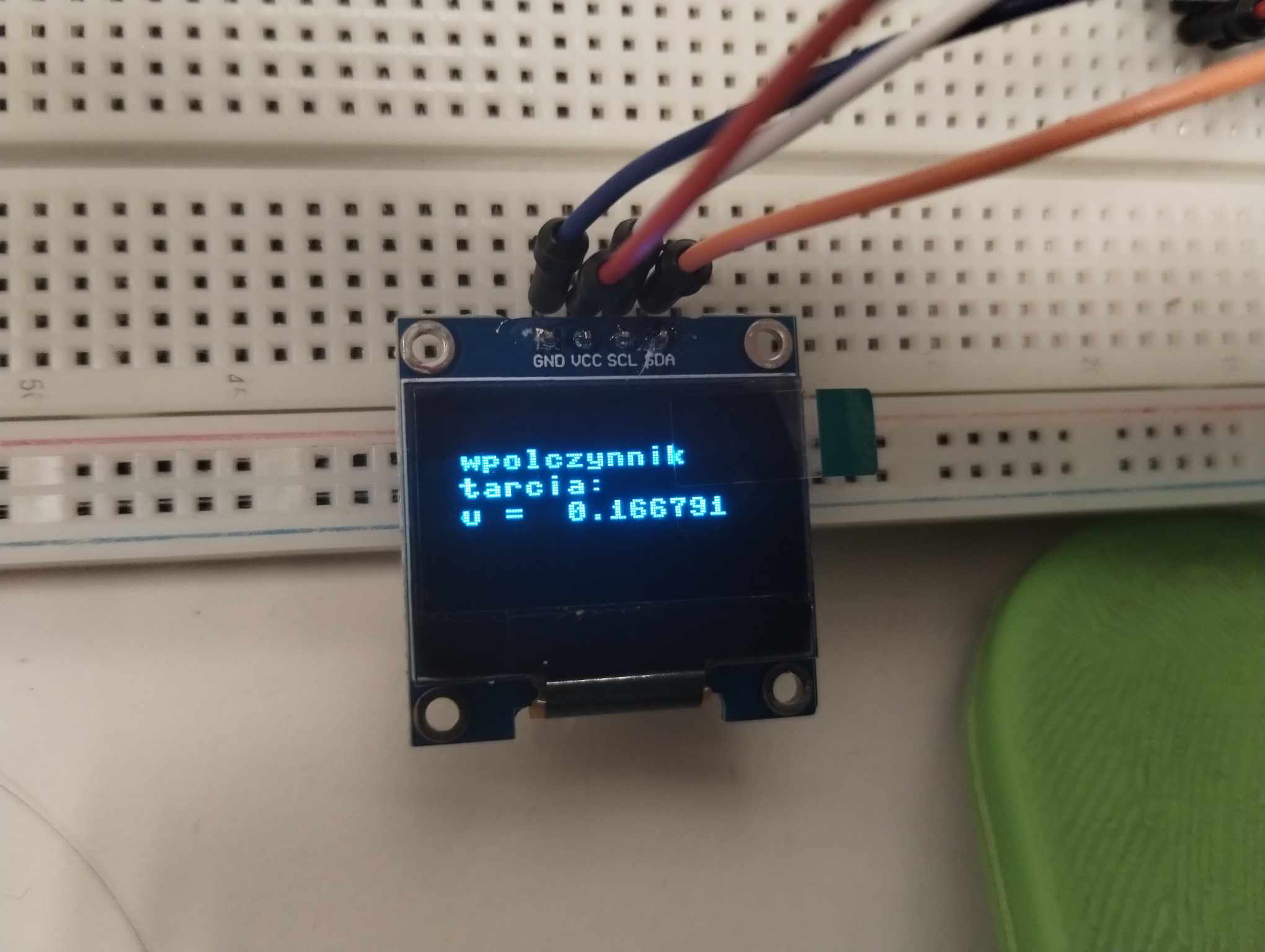
Teraz mamy już wszystko aby obliczyć nasz współczynnik tarcia, program wyświetli obliczoną wartość zarówno w konsoli w programie Thonny jak i na wyświetlaczu OLED l2c.
Na koniec warto wspomnieć o wyniku który podaje układ. Nie zawsze będzie on zgodny z rzeczywistością, dzieje się tak ponieważ układ jest bardzo wrażliwy na wszelkiego rodzaju niedoskonałości. Największym problemem jest sam dalmierz który po mimo uśredniania wyniku nie wykonuje wystarczająco dokładnych pomiarów. Na dodatek na wynik może też wpłynąć niedokładność konstrukcji rampy, nierównomierne rozłożenie masy obiektu zjeżdżającego lub nierównomierność powierzchni rampy. Ważne jest aby wykonać serie pomiarową oraz odrzucić wyniki nie mające kompletnego sensu.


import machine, time, math
from machine import Pin, I2C
import ssd1306
class HCSR04:
def __init__(self, trigger_pin, echo_pin, echo_timeout_us=500*2*30):
self.echo_timeout_us = echo_timeout_us
# Init trigger pin (out)
self.trigger = Pin(trigger_pin, mode=Pin.OUT, pull=None)
self.trigger.value(0)
# Init echo pin (in)
self.echo = Pin(echo_pin, mode=Pin.IN, pull=None)
def _send_pulse_and_wait(self):
self.trigger.value(0) # Stabilize the sensor
time.sleep_us(5)
self.trigger.value(1)
# Send a 10us pulse.
time.sleep_us(10)
self.trigger.value(0)
try:
pulse_time = machine.time_pulse_us(self.echo, 1, self.echo_timeout_us)
return pulse_time
except OSError as ex:
if ex.args[0] == 110: # 110 = ETIMEDOUT
raise OSError('Out of range')
raise ex
def distance_mm(self):
pulse_time = self._send_pulse_and_wait()
mm = pulse_time * 100 // 582
return mm
def distance_cm(self):
pulse_time = self._send_pulse_and_wait()
cms = (pulse_time / 2) / 29.1
return cms
def distance_m(self):
pulse_time = self._send_pulse_and_wait()
cms = (pulse_time / 2) / 29.1
ms=cms/100
return ms
#tu zacznij pisac swoj kod
i2c = I2C(scl=Pin(13), sda=Pin(15))
oled = ssd1306.SSD1306_I2C(128,64,i2c)
oled.fill(0)
counter = 0;
sensor = HCSR04(trigger_pin=5, echo_pin=4, echo_timeout_us=10000)
while True:
s=0
for i in range(10):
s=s+sensor.distance_m()
time.sleep(0.01)
s=s/10
print(s)
if(s<=0.3 and s>=0.1):
counter=counter+1
if(counter == 1):
s0 = s
else:
if(s<0.1):
sn = s
czas=counter*0.1
droga = s0-sn
break
print("czas: ", czas)
print("droga: ", droga)
g = 9.81
a = (2*droga)/(czas*czas)
#Tu wprowadź wymiary rampy
l=38 #długość
h=11.5 #Wysokość
alfa = math.asin(h/38)
u = math.tan(alfa) - (a/(g*math.cos(alfa)))
print("przys: ", a)
print("kat: ", (alfa*360/(2*3.14)))
print("wsp tarcia: ", u)
oled.text('wpolczynnik', 5, 14, 1)
oled.text('tarcia: ', 5, 24, 1)
oled.text('u = ', 5, 34, 1)
mi = str(u)
oled.text(mi, 45, 34, 1)
oled.show()